Geometría:
Se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos (que incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.).
Ejercicios:
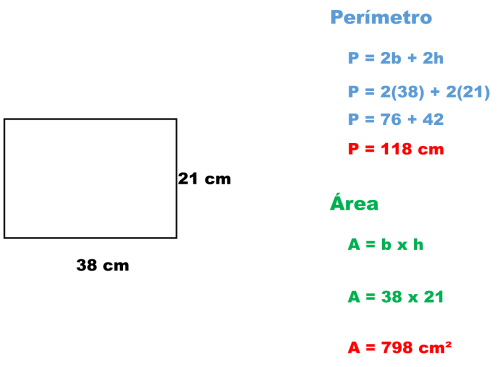
1) Una tapa de zapatos que mide 38 cm de largo por 21 cm de ancho. Sacar su perímetro y su área
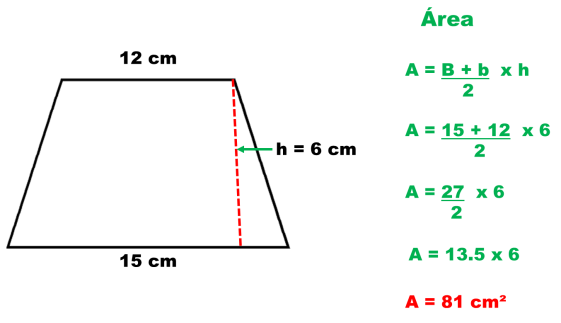
2) Un trapecio cuyas bases miden 12 y 15 cm y de altura mide 6 cm. Calcular su área
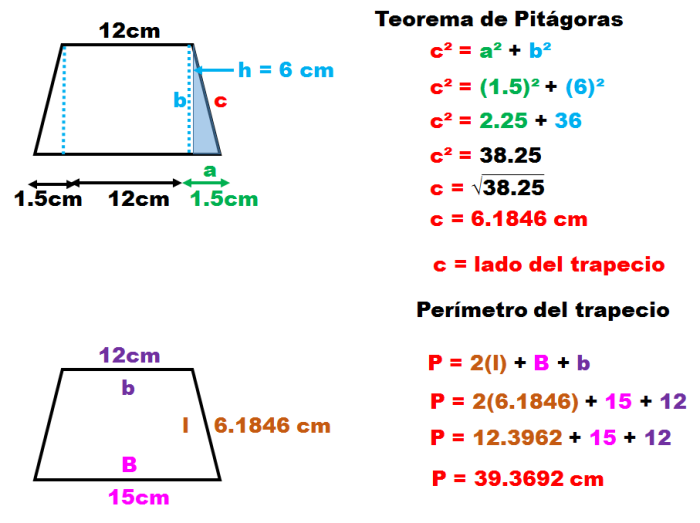
Al trazar el trapecio con las medidas conocidas, puedo saber la medida de su lado utilizando el Teorema de Pitágoras para obtener el perímetro.
3) Obtener la longitud de un arco de circunferencia cúyo ángulo central mide 82° y su radio 3,41cm
𝛑= 3,14 L= 2 . 𝛑 . r
L= 2 . 3,14 . 3,41
L= 21,41 cm
A 360° le corresponden 21,41cm ¿Cuánto le corresponde a 82°?
360° 82° x= 21,41 . 82
21,41cm x cm 360
x= 1.755,62
360
x= 4.876cm
4) Hallar el perímetro y el área de un triángulo sabiendo que la base mide 6.8m y la altura 9.3m
Sacamos la mitad de la base que es de 3, 4cm y realizamos el teorema de pitágoras
2 2 2
c = a + b
2 2 2
c = 3,4 + 9,3
2
c = 11,56 + 86, 49
2
c = 98,05
c = √98,05
c = 9,90m
Obtengo el perímetro y el área del triangulo
P= 1 + 2 (I) A= b . h
2
P= 6,8 + 2(9,90) A= 6,8 . 9,3
2
P= 6,8 + 19,80 A= 63,24
2 2
P= 26,6m A= 31,62m
No hay comentarios.:
Publicar un comentario