Función Cuadrática:
El modelo de esta función es:
2
F(x) = a.x + b.x + c
Recibe este nombre porque un término esta elevado al cuadrado. Su dominio e imagen es |R
Ejemplo:
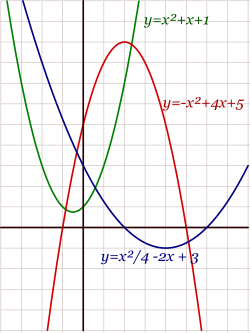
Ejercicios:
1) Determinar Dominio y Rango de f(x) = x2 - 2x – 3
Ahora ubicamos cada pareja en el plano y unimos los puntos para obtener la gráfica de nuestra función.

El vértice de una función cuadrática se define como (-b /2a, f(-b, 2a)) reemplazando valores tenemos que -b /2a = (-(-2) / 2(1)) = 1. Este es el valor de x en el vértice.
Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice:
f(1) = 12 - 2(1) – 3 = 1- 2 - 3 = - 4
Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice:
f(1) = 12 - 2(1) – 3 = 1- 2 - 3 = - 4
Por lo tanto, el vértice está en el punto (1, - 4).
El eje “Y” empieza a tomar valores (de abajo hacia arriba) a partir de -4.
Rango = [– 4 , + ∞ )
2) Determinar Dominio y Rango de f(x) = – x2 + 5x - 4
Ahora ubicamos cada pareja en el plano y unimos los puntos para obtener la gráfica de nuestra función.

El vértice está en (-b /2a, f(-b, 2a)) reemplazando valores tenemos que -b /2a =( - 5 / 2(-1)) = 5/2 (o 2,5). Este es el valor de x en el vértice.
Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice:
f(5/2) = -(5/2)2 + 5(5/2) – 4 = -25/4 + 25/2 - 4 = 9/4 = 2,25
Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice:
f(5/2) = -(5/2)2 + 5(5/2) – 4 = -25/4 + 25/2 - 4 = 9/4 = 2,25
Por lo tanto, el vértice está en el punto (2.5; 2,25).
El eje “Y” empieza a tomar valores (de abajo hacia arriba) desde menos infinito y llega hasta el vértice de la parábola (hasta Y = 2,25).
Rango = [– ∞ , 2.25 )
3) Representa gráficamente la función cuadrática:
y = -x² + 4x - 3
1. y = −x² + 4x − 3
a) Vértice
x v = − 4/ −2 = 2 y v = −2² + 4· 2 − 3 = 1 V(2, 1)
b) Puntos de corte con el eje OX.
x² − 4x + 3 = 0
 (3, 0) (1, 0)
(3, 0) (1, 0)
c) Punto de corte con el eje OY.
(0, −3)

4) Partiendo de la gráfica de la función f(x) = x2, representa:
a) y = x² + 2
b) y = x² − 2
c) y = (x + 2)²
d) y = (x − 2)²
e) y = (x − 2)² + 2
f) y = (x + 2)² − 2

y = x²


y = x² + 2 y = x² − 2


y = (x + 2)² y = (x − 2)²


y = (x − 2)² + 2 y = (x + 2)² − 2
No hay comentarios.:
Publicar un comentario