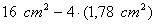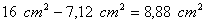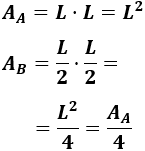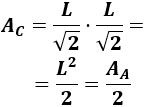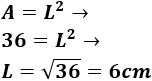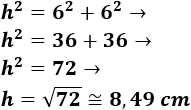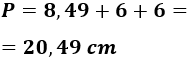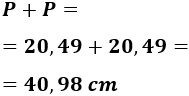Área: permite asignar una medida a la extensión de una superficie, expresada en matemáticas como unidades de medida denominadas unidades de superficie. El área es un concepto métrico que requiere la especificación de una medida de longitud.
Ejercicios:
1) En la figura se tiene un cuadrado de lado l = 4 cm. En las esquinas se tiene 4 cuadrados de lado l/3.
Calcular el área de la región sombreada
a) Cálculo del área del cuadrado de l = 4 cm :
A = l2 = (4cm)2 = 16 cm2
= l2 = (4cm)2 = 16 cm2
b) Cálculo del área del cuadrado de lado l/3:
A? = 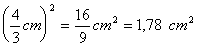
c) Cálculo del área de la región sombreada
Área Sombreada =
= 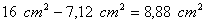
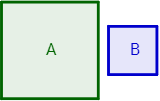
2) Se tienen dos cuadrados: el cuadrado A y el cuadrado B:
Si el lado del cuadrado B mide la mitad del lado del cuadrado A, ¿el área del cuadrado B es la mitad del área del cuadrado A?
No, el área del cuadrado B es la cuarta parte del área del cuadrado A.
Si el lado de A mide L, el lado de B mide L/2. Por tanto, sus áreas son:
El cuadrado C cuya área es la mitad del cuadrado A es el de lado L/√2:
Perímetro: es la suma de las longitudes de los lados de una figura geométrica plana.
Ejercicios:
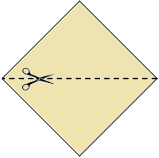
Se tiene una cartulina cuadrada cuya área es igual a 36cm2. Si se corta la cartulina por una de sus diagonales, ¿cuánto vale la suma de los perímetros de los dos triángulos que se obtienen?
La hipotenusa del triángulo es la diagonal del cuadrado y sus catetos son los lados.
Calculamos el lado L del cuadrado a partir de su área:
Por tanto, los catetos del triángulo miden 6cm cada uno.
Aplicamos el teorema de Pitágoras para calcular la hipotenusa h del triángulo rectángulo:
Por tanto, la hipotenusa mide aproximadamente 8,49 centímetros.
El perímetro del triángulo es
Como los triángulos son iguales, la suma de sus perímetros es:
Raíz Cuadrada: la raíz cuadrada de un número x, es el número y que al ser multiplicado por sí mismo
Ejercicios:
Indica si es verdadero o falso y justifica tu respuesta:
a) √8.3 = √8 . √3
b) √9+6 = √9 + √6
c) √100-36 = √100 - √36
d) 3√125:8 = 3√125 : 3√8
e) 6√3√2 = 9√2
a) Verdadero: la multiplicación dentro de una raíz es igual que multiplicarla por separado
b) Falso: cuando esta sumando, no se pueden separar
c) Falso: cuando esta restando, no se puede separar
d) Verdadero: la división dentro de una raíz, es igual que dividirlo por separado
e) Falso: se multiplican los índices
Cuadro Mágico: tabla de grado primario donde se dispone de una serie de números enteros en un cuadrado o matriz de forma tal que la suma de los números por columnas, filas y diagonales principales sea la misma.
Ejercicios:
A. Los cuatro cuadrados siguientes de orden tres son mágicos pero le faltan valores en algunas celdas. Completar con los números que faltan.
A.1.-Sumamos los elementos de la diagonal principal, 12 + 15 + 18 = 35; Por tanto, el número mágico es 35 en el primer cuadrado mágico.
La primera fila será: 12, 17, 35 - (12+17) = 6;
La segunda columna será:17, 15, 35 – (17 + 15) = 3;
La tercera columna será: 6, 35–(6+18) = 11, 18;
La segunda fila es:35 - (15 + 11) = 9, 15, 11;
La tercera fila será: 35 – (3 + 18) = 14, 3, 18;
La diagonal secundaria será:14, 15, 6.





































 = l2 = (4cm)2 = 16 cm2
= l2 = (4cm)2 = 16 cm2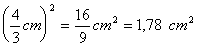
 = A
= A