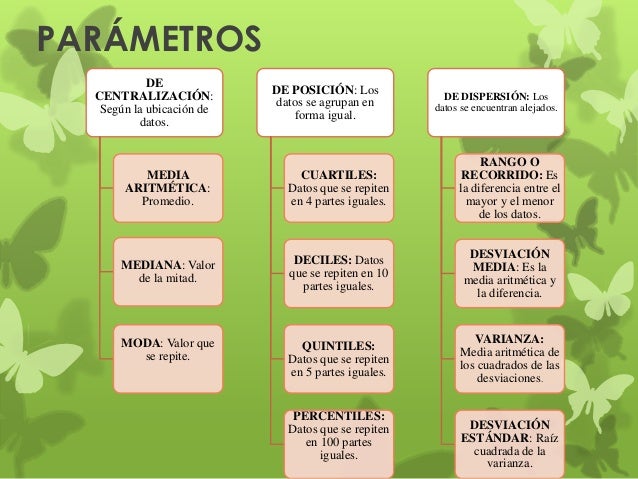
Parámetros Estadísticos:
Es un número que resume la gran cantidad de datos que pueden derivarse del estudio de una variable estadística. El cálculo de este número está bien definido

Ejercicios:
1) Calcular la media, la mediana y la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
Xi fi Fi Xi . fi
2 2 2 4 Moda: 5
3 2 4 6
4 5 9 20 Mediana: 20/2=10
5 6 15 30 Me: 5
6 2 17 12 Media: X = 96 = 4,8
8 3 20 24 20
20 96
2) El número de libro leídos por los miembros de un círculo de lectores, a lo largo de un mes, viene dado por la siguiente tabla. Hallar la moda
Número de libros Xi: 1 2 3 4 5 6 7
Número de personas fi: 5 12 18 11 7 4 1
La moda es el valor con mayor frecuencia, por tanto: 5 3 libros
3) Al abrir la biblioteca del Centro Cultural de un pueblo, entren 11 personas cuya edad media es 32 años. Una hora más tarde, no había salido nadie y habían 7 personas más, siendo ahora 39 años la edad media. Entonces, entra un joven y la edad se reduce a 38 años. ¿Cuántos años tiene el joven?
Calculamos las sumas de las edades de las personas que hay en cada momento. De los incrementos de estas sumas se deduce la edad de la última persona que entra
32 . 11 = 352 39 . 18 = 702 38 . 19 = 722
722 - 702 = 20 años
4) Determina la mediana de la distribución:
Altura Número de plantas Fi
[0,5) 3 3
[5,10) 6 9
[10,15) 7 16
[15,20) 4 20
La mitad del número de datos es 20 = 10, luego la clase mediana es [10,15), ya que es la
2
primera cuya frecuencia acumulada supera ese valor. La mediana es la marca de esta clase:
M - 12,5





![Li-1 - Li ni[18; 25) 22[25; 35) 48[35; 45) 51[45; 55) 36[55; 65] 27 ...](https://image.slidesharecdn.com/afbe9d01-120327214802-phpapp01/95/ejercicios-resueltos-de-estadstica-4-728.jpg?cb=1333530847)
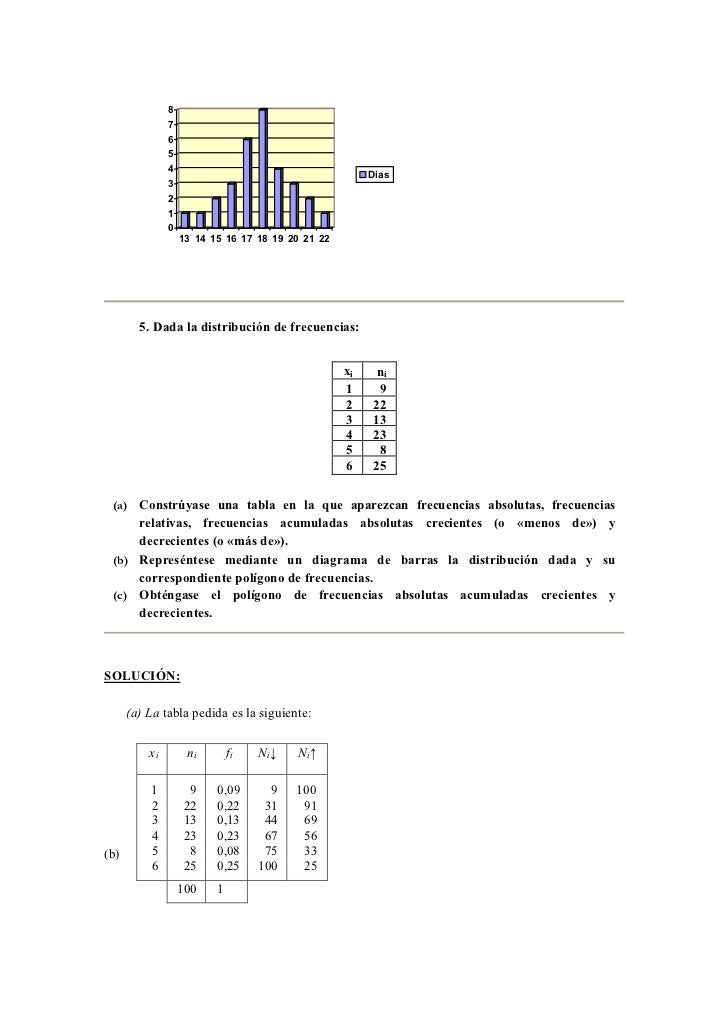
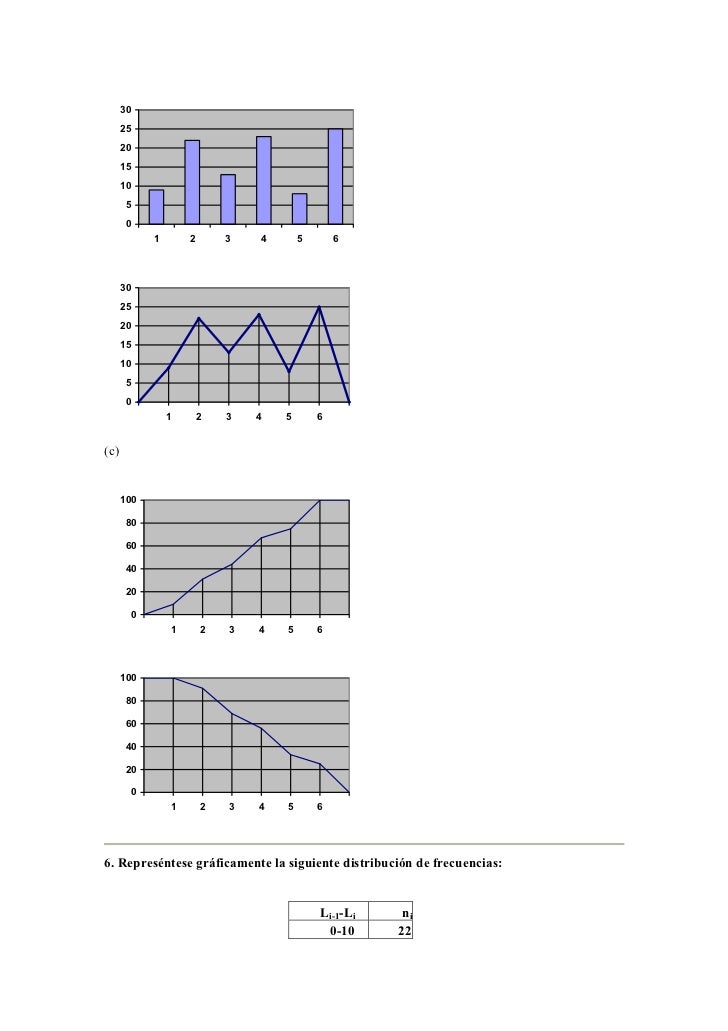

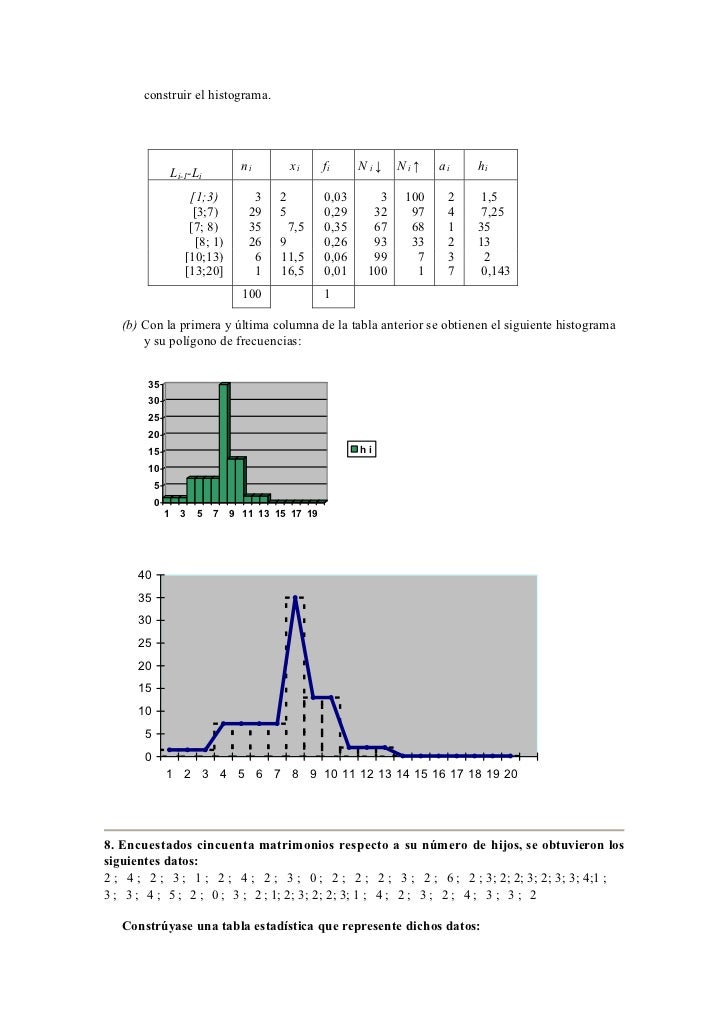 X1 N1
X1 N1