Números Reales (II)

Sucesiones: 

Es una aplicación cuyo dominio es el conjunto de los números naturales y su condominio es cualquier otro conjunto, generalmente de números, figuras geométricas o funciones. Cada uno de ellos es denominado termino (también elemento o miembro) de la sucesión y al número de elementos ordenados (posiblemente infinitos) se le denomina la longitud de la sucesión.

Características:

• En función del número que tengan, las sucesiones pueden ser finitas o infinitas.
• Crecientes si cada término es mayor que su anterior, es decir
  
  $$a_n\le a_{n+1}$$
  O decrecientes si
  
  $$a_n\ge a_{n+1}$$
• Son aritméticas cuando cada término es la suma del término anterior más un número constante, al que llamamos diferencia y denotamos por d. Es decir,
  
  $$a_{n+1}=a_n+d$$
• Son geométricas cuando cada término es el término anterior multiplicado por un número constante, al que llamamos razón y denotamos por r . Es decir,
  
  $$a_{n+1}=a_n\cdot r$$

Fórmulas

SUCESIÓN ARITMÉTICA
Es de la forma
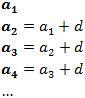Diferencia	Término general
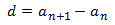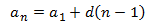Suma de los n primeros términos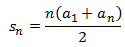
SUCESIÓN GEOMÉTRICA
Es de la forma
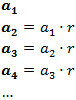Razón	Término general
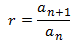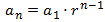Suma de los n primeros términos	Suma de todos los términos

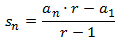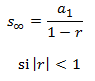Ej: a1 es el primer termino, a2 es el segundo termino, a3 es el tercer termino... an es el n-esimo termino 

Problema: Demostrar que la suma infinita de la sucesión

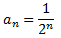
                   es 1 con la ayuda del siguiente diagrama que representa un cuadrado de lado 1.

Calculamos los primeros términos de la sucesión:

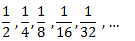
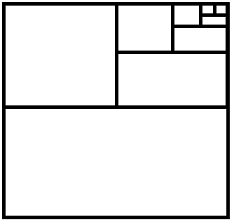
Puesto que el lado del cuadrado es 1, su área es 1. Así, el área de la mitad del cuadrado es 1/2. El área de la mitad de esta mitad es 1/4. Y así, sucesivamente:

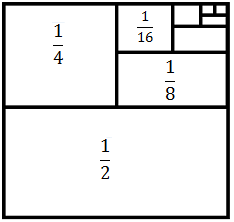
Las áreas de los cuadrados o rectángulos que se obtienen al dividir por la mitad son los términos de la sucesión. Para infinito, habremos recubierto el cuadrado completo, que tiene área 1. Por tanto, la suma de todos los términos de la sucesión es 1.